14. Kinetics Estimation

This section gives in-depth descriptions of algorithms used for determining kinetic parameters. For general usage of the kinetic database see Kinetics Database.

14.1. Priority of Kinetic Databases

When multiple sources are available for kinetic parameters, the following priority is followed:

1. Seed mechanisms (based on listed order in input.py)

2. Reaction libraries (based on listed order in input.py)

3. Matched training set reactions

4. Exact template matches from rules or matched training groups (based on rank)

5. Estimated averaged rules

In the case where multiple rules or training set reactions fall under the same template node, we use a user-defined rank to determine the priority of kinetic parameters

Rank	Example methods
Rank 1	Experiment/FCI
Rank 2	W4/HEAT with very good (2-d if necessary) rotors
Rank 3	CCSD(T)-F12/cc-PVnZ with n>2 or CCSD(T)-F12/CBS with good (2-d if necessary) rotors
Rank 4	CCSD(T)-F12/DZ, with good (2-d if necessary) rotors
Rank 5	CBS-QB3 with 1-d rotors
Rank 6	Double-hybrid DFT with 1-D rotors
Rank 7	Hybrid DFT (w/ dispersion) (rotors if necessary)
Rank 8	B3LYP & lower DFT (rotors if necessary)
Rank 9	Direct Estimate/Guess
Rank 10	Average of Rates
Rank 0	General Estimate (Never used in generation)

The rank of 0 is assigned to kinetics that are generally default values for top level nodes that we have little faith in. It is never used in generation and its value will in fact be overriden by averages of its child nodes, which generates an averaged rate rule with rank 10.

Only non-zero rules are used in generation. A rank of 1 is assigned to the most trustworthy kinetics, while a rank of 10 is considered very poor. Thus, a rate rule of rank 3 will be given priority over a rate rule of rank 5.

Short Glossary:

FCI (Full Configuration Interaction): Exact solution to Schrodinger equation within the chosen basis set and Born-Oppenheimer approximation; possible for about 12 electrons with reasonably sized basis set (cost grows factorially with number of electrons).

Wn (Weizmann-n): Composite methods often with sub-kJ/mol accuracies; W1 is possible for about 9 heavy atoms; W1 aims to reproduce CCSD(T)/CBS; W4 aims to reproduce CCSDTQ5/CBS.

HEAT (High Accuracy Extrapolated ab inito thermochemistry): Sub-kJ/mol accuracies; essentially CCSDTQ with various corrections; similar in cost to Wn.

CBS (Complete Basis Set): Typically obtained by extrapolating to the complete basis set limit, i.e., successive cc-pVDZ, cc-pVTZ, cc-pVQZ, etc. calculations with some extrapolation formula.

CCSD(T)-F12: Coupled cluster with explicit electron correlation; chemical accuracy (1 kcal/mol) possible with double-zeta basis sets.

14.2. Kinetic Families

To show the algorithm used by kinetic families, the following H-abstraction will be used an example

First the reacting atoms will be identified. Then, the family`s trees will be descended as far as possible to give the reaction`s groups.

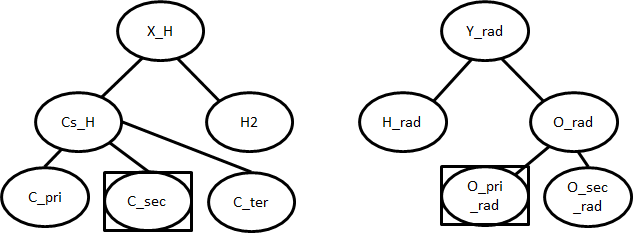
Using the sample tree shown above, the desired template is (C_sec, O_pri_rad). The algorithm will then search the database for parameters for the template. If they are present, an exact match will be returned using the kinetics of that template. Note that an exact match refers to the nodes (C_sec, O_pri_rad) and not the molecules (propane, OH).

There may not be an entry for (C_sec, O_pri_rad) in the database. In that case, the rule will attempt to “fall up” to more general nodes:

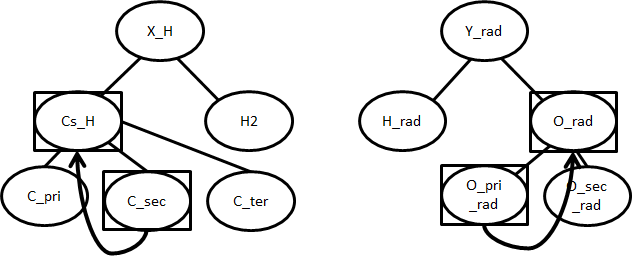
Now the preferred rule is (Cs_H, O_rad). If database contains parameters for this, those will be returned as an estimated match.

If there is still no kinetics for the template, the entire set of children for Cs_H and O_rad will be checked. For this example, this set would include every combination of {C_pri, C_sec, C_ter} with {O_pri_rad, O_sec_rad}. If any these templates have kinetics, an average of their parameters will be returned as an estimated match. The average for \(A\) is a geometric mean, while the average for \(n\), \(E_a\), and \(\alpha\) are arithmetic means.

If there are still no “sibling” kinetics, then the groups will continue to fall up to more and more general nodes. In the worst case, the root nodes may be used.

Kinetic averaging takes into account the nodal distances (the distance between a child node and its parent). By default, the nodal distance is 1, but custom values can be specified within a group.py file, in order of ascending precedence: either in a list of values for each tree e.g. treeDistances = [1,2,5], or directly assigned to an entry in the group definition e.g. Entry(... nodalDistance=5, ). This may be desired in special cases where one or more child nodes matches the family but has very different kinetics, leading to poor overall tree estimates.

A Full List of the Kinetics Families in RMG is available.

14.3. Reverse Rates

Rates in the reverse direction are calculated from the forward rate (as defined by the family) and the equilibrium constant (as calculated from thermodynamic parameters).

14.4. Reaction Comments

Reaction comments are saved by RMG to the chem_annotated.inp Chemkin input file. These comments contain information about the source of the reaction rate and are read by RMG when loading the Chemkin file. These comments are compiled from many different locations in the code.

Comments attached to the kinetics attribute of the entry used are included first. These can occur if there is a comment hard-coded in the kinetics database, or if the rate rule was derived from a training reaction, in which case From Training reaction # for rate rule ## is automatically added. Then, comments describing the match are added based on the details of how the kinetics were estiamted. Finally, additional metadata about the reaction type are included.