1. Rate-based Model Enlarging Algorithm

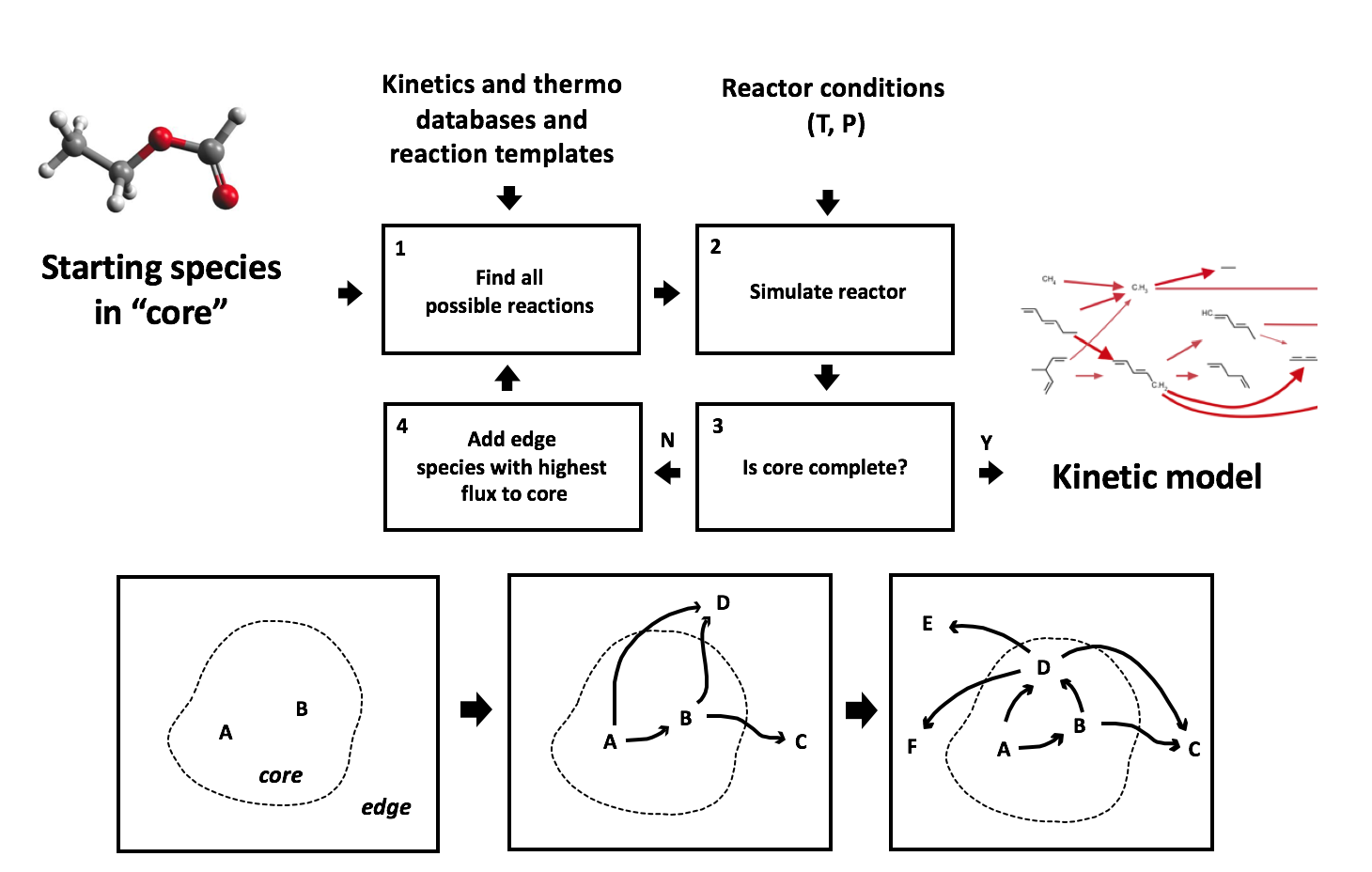
To construct a mechanism, the user must specify an initial set of species and the initial conditions (temperature, pressure, species concentrations, etc.). RMG reacts the initial species in all possible ways according to its known reaction families, and it integrates the model in time. RMG tracks the rate (flux) at which each new “edge” species is produced, and species (and the reactions producing them) that are produced with significant fluxes are incorporated into the model (the “core”). These new core species are reacted with all other core species in the model to generate a new set of edge species and reactions. The time-integration restarts, and the expanded list of edge species is monitored for significant species to be included in the core. The process continues until all significant species and reactions have been included in the model. The definition of a “significant” rate can be specified by the user by taking the following definition for a single species rate:

\(R_i = \frac{dC_i}{dt}\)

and the following definition for the reaction system’s characteristic rate, which is the sum of all core species rates:

\(R_{char} = \sqrt{\sum\limits_{j} R_{j}^2}\quad \quad \textrm{species $j$ $\in$ core}\)

When a \(\textrm{species $i$ $\in$ edge}\) exceeds a “significant” rate equal to \(\epsilon R_{char}\), it is added to the core. The parameter \(\epsilon\) is the user-specified toleranceMoveToCore that can be adjusted under the model tolerances in the RMG Input File.

For more information on rate-based model enlargement, please refer to the papers [Gao2016] or [Susnow1997].

[Gao2016]

C. W. Gao, J. W. Allen, W. H. Green, R. H. West, “Reaction Mechanism Generator: automatic construction of chemical kinetic mechanisms.” Computer Physics Communications (2016).

[Susnow1997]

R. G. Susnow, A. M. Dean, W. H. Green, P. K. Peczak, and L. J. Broadbelt. “Rate-Based Construction of Kinetic Models for Complex Systems.” J. Phys. Chem. A 101, p. 3731-3740 (1997).

1.1. Filtering Reactions within the Rate-based Algorithm

Filtering reactions in the react step in the flux-based algorithm attempts to speed up model generation by attacking the pain point. RMG has trouble converging when generating models for large molecules because it searches for reactions on the order of \((n_{reaction\: sites})^{{n_{species}}}\).

The original algorithm performs in the following manner:

1. Reacts species together (slow)

2. Determines which reactions are negligible (fast)

By filtering reactions we add a pre-filtering step before step 1 which prevents species from reacting together when the reactions are expected to be negligible throughout the simulation.

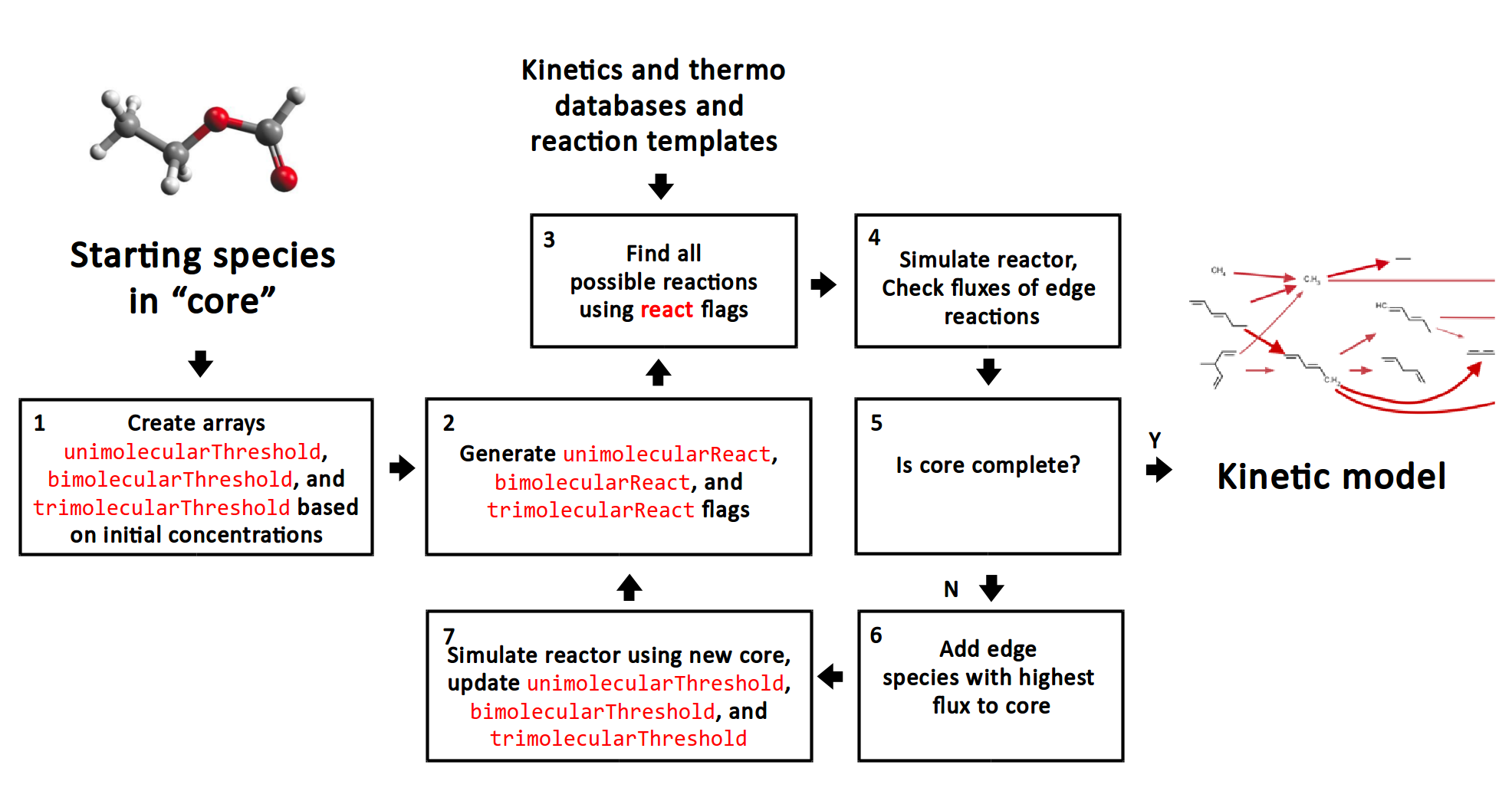
Here, unimolecularThreshold, bimolecularThreshold, and trimolecularThreshold are binary arrays storing flags for whether a species or a pair of species are above a reaction threshold. For a unimolecular rate, this threshold is set to True if the unimolecular rate of \(\textrm{reaction $k$}\) for a species A

\(R_{unimolecular} = k_{threshold}C_A > \epsilon R_{char}\)

at any given time \(t\) in the reaction system, where \(k_{threshold} = \frac{k_B T}{h}\)

For a bimolecular reaction occuring between species A and B, this threshold is set to True if the bimolecular rate

\(R_{bimolecular} = k_{threshold}C_A C_B > \epsilon R_{char}\)

where \(k_{threshold} = filterThreshold\). filterThreshold is set by the user in the input file and its default value is \(10^{8} \frac{m^3}{mol\cdot s}\). This is on the same order of magnitude as the collision limit for two hydrogen atoms at 1000 K. In general, it is recommended to set filterThreshold such that \(k_{threshold}\) is slightly greater than the maximum rate constants one expects to be present in the system of interest. This will ensure that very fast reactions are not accidentally filtered out.

Similarly, for a trimolecular reaction, the following expression is used:

\(R_{trimolecular} = k_{threshold}C_A C_B C_C > \epsilon R_{char}\)

where \(k_{threshold} = 10^{-3} \cdot filterThreshold \frac{m^6}{mol^2\cdot s}\). Based on extending Smoluchowski theory to multiple molecules, the diffusion limit rate constant for trimolecular reactions (in \(\frac{m^6}{mol^2\cdot s}\)) is approximately three orders of magnitude smaller than the rate constant for bimolecular reactions (in \(\frac{m^3}{mol\cdot s}\)). It is assumed here that Smoluchowski theory gives a sufficient approximation to collision theory in the gas phase.

When the liquid-phase reactor is used, the diffusion limits are calculated using the Stokes-Einstein equation instead. For bimolecular reactions, this results in

\(k_{threshold}[m^3/mol/s] = 22.2\frac{T[K]}{\mu[Pa\cdot s]}\)

and for trimolecular

\(k_{threshold}[m^6/mol^2/s] = 0.11\frac{T[K]}{\mu[Pa\cdot s]}\)

where \(\mu\) is the solvent viscosity. The coefficients in the above equations were obtained by using a representative value of the molecular radius of 2 Angstrom. More details on the calculation of diffusion limits in the liquid phase can be found in the description of liquid-phase systems under diffusion-limited kinetics.

Three additional binary arrays unimolecularReact, bimolecularReact, and trimolecularReact store flags for when the unimolecularThreshold, bimolecularThreshold, or trimolecularThreshold flag shifts from False to True. RMG reacts species when the flag is set to True.